Answer:
The true stress at true strain 0.05cm/cm is 80MPa
Step-by-step explanation:
Given that
the strength coefficient is K
true strain is ε
strain hardening exponent is n
initial diameter of bar is d = 1cm, (10mm)
tensile force is F
engineering stress(S) = 120
the engineering stress(S) =
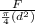
To find force (F) =
120 =
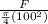
F = 120 * (π/4) * (100)
F = 9425N
Calculate the true strain (ε) = In (l₀ / l₁)
where
l₀ = initial length of the metallic bar = 3cm
l₁ = final length of metallic bar = 3.5cm
ε = In (3.5 / 3)
= In 1.1667
= 0.154cm/cm
Calculate the true stress (σ) at fracture point
=
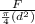
tensile force is F and final diameter of bar is d₁ (d in the eqn)
Substitute 9425 N for F and 0.926 cm (9.26mm) for d₁ (d in the eqn)
σ =
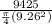
= 140MPa
To find the strength coefficient (K) of the material bar
K =

K =
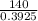
= 356.75MPa
To calculate the true stress σ true strain of 0.05cm/cm
K = 356.75MPa
σ =

=
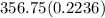
= 80MPa
The true stress at true strain 0.05cm/cm is 80MPa