Question

A 10 cm long thin glass rod uniformly charged to 10 nC and a 10 cm long thin plastic rod uniformly charged to 10 nC are placed side by side 4.0 cm apart What are the electric field strengths E1 to E3 at distances 1.0 cm 2.0 cm and 3.0 cm from the glass rod along the line connecting the midpoints of the two rods

Answer 1

E1=119834 V/m; E2=0 V/m; E3=-119834 V/m- it has opposite direction to E1- read explanation

Step-by-step explanation:

In order to solve this problem, we should consider several factors:

1) direction of the individual electric fields, created by the glass and plastic rods;

2) magnitude of these fields at the given points. Please, note, that E1 is located 1cm from the glass and 3cm from the plastic rod, E2 is located at a distance of 2 cm from both rods and E3 has opposite distance to E1 point.

There are two approaches to calculate electric field of the rod:

1) we can separate a rod into infinitely small pieces with charges and calculate their total field using integration;

2) we can use Gauss law:
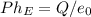`Ph_(E)=Q/e_(0)`, where Ph is the flux of the electric field, Q- is the total charge inside the given enclosed area and e0- dielectric constant. This approach can be used, as we are calculating values for the midpoint, where the field is balanced with respect to the y-axis. Once the problems are covering not a mid point, integration will yield the answer quicker.

Flux of the field can be calculated as:
`Ph= E*A*cos\alpha`

Where E- electric field, A- enclosed area, cosα- angle, between the normal to the surface and direction of E.

In case of the rods, the enclosed surface, which covers a rod at a specific distance can be represented as a cylinder. Considering, that the point, for which we need to calculate the field is located on the distance x from the rod and the rod has its length l, area of such cylinder can be calculated, as:

`A=2\pi xl`

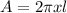
Using this approach, we can now calculate the magnitude of the electric field, produced by each individual rod.

In order to calculate the total field, we should also consider directions of the vectors E. As both rods have positive charges, the lined of E are directed away from the rods. In the area, between the rods, the vectors have opposite direction- E of the glass rod is directed towards the plastic one and vice versa. For this case, the final value of the field has to be calculated as:
`E=E_(Glass)-E_(Plastic)`. Note, that this equation can be used only for the given scenario with the mid-points, as y-components of the fields are zero.

Now we can calculate the fields of each rod and the total value of the field:

`E*2\pi xL=Q/e_(0) \\E=(Q)/(2\pi xLe_(0) )\\`

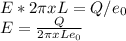
Now, we can calculate numerical values of the individual fields, using e0=8.854*10^(-12)

For the glass rod: E1=179751 V/m; E2=89875.51 V/m; E3=59917.01 V/m

For the plastic rod: E1=59917.01 V/m; E2=89875.51 V/m; E3=179751 V/m

As a result, the total electric field:

E1=119834 V/m and it is directed towards the plastic rod away from the glass rod;

E2=0 V/m- the fields balance each other;

E3=110834 V/m and it is directed towards the glass rod and away from the plastic rod.