Answer:
Therefore, the volume of the cone is V=4π.
Explanation:
From task we have a circular cone with radius 2 m and height 3 m. We use the disk method to find the volume of this cone.
We have the formula:
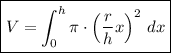
We know that r=2 and h=3, and we get:
![V=\int_0^3\pi \cdot \left((2)/(3)x\right)^2\, dx\\\\V=\int_0^3 \pi (4)/(9)x^2\, dx\\\\V= (4\pi)/(9) \int_0^3 x^2\, dx\\\\V= (4\pi)/(9) \left[(x^3)/(3)\right]_0^3\, dx\\\\V= (4\pi)/(9)\cdot 9\\\\V=4\pi](https://img.qammunity.org/2021/formulas/mathematics/college/7rqoauo160gl688dpnnc6vr6h1krrup3yc.png)
Therefore, the volume of the cone is V=4π.