Question

A store gives a customer 20% off if $10 or more amount of product is purchased. Otherwise the customer pays the usual price at checkout. The amount of product a customer purchases is modeled by a continuous random variable X with density

Answer 1

The expected payment by the customer at the checkout is $9.

Explanation:

The amount of the product is given as

`f(x)=\left \{ {{(50)/(x^3) \,\,\,\,\, x\geq 5 } \atop {0}} \right.`

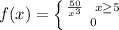
Now the expected payment is given as

`EP=\int\limits^(10)_(5) {x f(x)} \, dx +\int\limits^(\infty)_(10) {0.8x f(x)} \, dx`

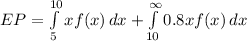
Here 0.8 x is used in the second integral because of the discount of 20% i.e. the expected price is 80% of the value such that

`\\EP=\int\limits^(10)_(5) {x (50)/(x^3)} \, dx +\int\limits^(\infty)_(10) {0.8x (50)/(x^3)} \, dx\\\\EP=\int\limits^(10)_(5) {(50)/(x^2)} \, dx +\int\limits^(\infty)_(10) {(40)/(x^2)} \, dx\\EP=[(50)/(-x)]_5^(10) +[(40)/(-x)]_(10)^(\infty) \\EP=[(-50)/(10)+(50)/(5)] +[(-40)/(\infty)+(40)/(10)]\\\\EP=-5+10+0+4\\EP=9`

The expected payment by the customer at the checkout is $9.