Question

A three-point bending test was performed on an aluminum oxide specimen having a circular cross section of radius 5.0 mm (0.20 in.); the specimen fractured at a load of 3000 N (675 lb) when the distance between the support points was 40 mm (1.6 in.). Another test is to be performed on a specimen of this same material, but one that has a square cross section of 15 mm (0.6 in.) length on each edge. At what load would you expect this specimen to fracture if the support point separation is maintained at 40 mm (1.6 in.)?

Answer 1

The load is 17156 N.

Step-by-step explanation:

First compute the flexural strength from:

σ = FL / π
`R^(3)`

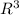
= 3000
`*` (40
`*` 10^-3) / π (5
`*` 10^-3)^3

σ = 305
`*` 10^6 N / m^2.

We can now determine the load using:

F = 2σd^3 / 3L

= 2(305
`*` 10^6) (15
`*` 10^-3)^3 / 3(40
`*` 10^-3)

F = 17156 N.