Answer:
Part a: The energy absorbed is inversely proportional to its mass.
Part b: The energy absorbed by auto A is 180kJ and that of energy absorbed by the auto B is 320 kJ.
Step-by-step explanation:
Part a:
Consider the case before collision which is given as
Let v be the velocity of center of Mass G
By the conservation of momentum
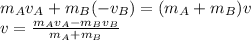
Now the relative motion of A wrt G, the velocity is given as
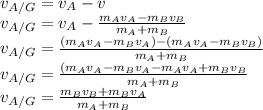
Similarly the relative motion of auto B wrt G, the velocity is given as

Now the Kinetic Energies are given as
For the auto A
![K.E_(A/G)=(1)/(2)m_Av_(A/G)^2\\K.E_(A/G)=(1)/(2)[m_A(m_Bv_B+m_Bv_A)/(m_A+m_B)]^2\\K.E_(A/G)=(1)/(2)(m_Am_B^2(v_A+v_B)^2)/((m_A+m_B)^2)](https://img.qammunity.org/2021/formulas/engineering/college/vy08l511knordgehopndhdye83jg1fyysa.png)
For the auto B
![K.E_(B/G)=(1)/(2)m_Bv_(B/G)^2\\K.E_(B/G)=(1)/(2)[m_B(m_Av_B+m_Av_A)/(m_A+m_B)]^2\\K.E_(B/G)=(1)/(2)(m_Bm_A^2(v_A+v_B)^2)/((m_A+m_B)^2)](https://img.qammunity.org/2021/formulas/engineering/college/scpmorun7ev4r9exlgmjlhezimpjpkj0zf.png)
Now the case after collision relates that
As there is no external force the G is moving along the whole system thus
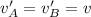
Or
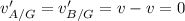
Similarly
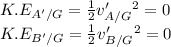
So the energy absorbed are given as
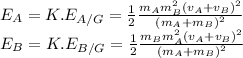
Now taking the ratio of these values as
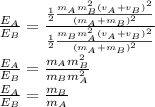
So The energy absorbed is inversely proportional to its mass.
Part b
Mass of car A=m_a=1600 kg
Mass of car B=m_b=900 kg
Velocity of car A=v_a=90 km/h=25 m/s
Velocity of car B=v_b=60 km/h=16.67 m/s
Now the energy absorbed by the car A is given as
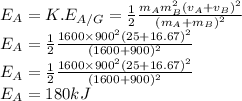
Now the energy absorbed by the car B is
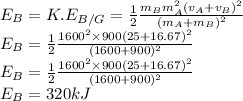
So the energy absorbed by auto A is 180kJ and that of energy absorbed by the auto B is 320 kJ.