Answer:
Part b: The number of ways in which there will be four aces is 1677106641
Part c: The number of ways in which there will be at least one ace is 442085310304
Part d: The number of ways in which cards can be dealt is 635013559600
Explanation:
Part b
The number of different bridge hands with four aces is
As Total Number of Hands with 4 aces is given as
As the order does not matter, thus the number of Hands with 4 aces is given as
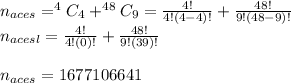
So the number of ways in which there will be four aces is 1677106641
Part c
Total cards without ace = 48
Number of hands of (no ace) =
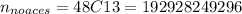
Number of hands of (at least one ace)

So the number of ways in which there will be at least one ace is 442085310304
Part d
As Total Number of Hands is given as
Total Cards=52
Cards per Player=13
As the order does not matter, thus the number of Hands is given as
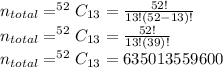
So the number of ways in which cards can be dealt is 635013559600