Question

Argon is compressed in a polytropic process with = 1:3 (i.e., PV = costant) from 120 kPa and 10 C until it reaches a temperature of 120 C in a piston{cylinder device. Model the system as an ideal gas and determine the speci c work (work per unit mass) done by the gas and the heat per unit mass transferred during this the process.

Answer 1

The work done per unit kg of mass is -76.08 kJ/kg while the heat transferred per unit kg of mass is -42.01 kJ/kg.

Step-by-step explanation:

For Argon the molar mass is given as

`M=40`

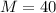
Now the gas constant for Argon is given as

`R=\frac{\bar{R}}{M}\\R=(8.314)/(40)\\R=0.208 kJ/K kg`

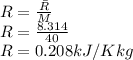
Initial Temperature is T_1=10 C=10+273=283 K

Final Temperature is T_2=120 C=120+273=393 K

Initial Pressure is P_1=120 kPa

The initial volume is given as

`v_1=(RT_1)/(P_1)\\v_1=(0.208* 283)/(120)\\v_1=0.491 m^3/kg`

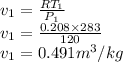
For the polytropic process with γ=1.3 is given as

`(P_2)/(P_1)=((T_2)/(T_1))^{(\gamma)/(\gamma-1)}\\(P_2)/(120)=((393)/(283))^{(1.3)/(1.3-1)}\\(P_2)/(120)=((393)/(283))^{(1.3)/(0.3)}\\(P_2)/(120)=((393)/(283))^{(1.3)/(0.3)}\\{P_2}=((393)/(283))^{(1.3)/(0.3) }* 120\\P_2=497.9 kPA`

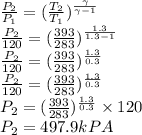
Now the volume at the second stage is given as

`v_2=(RT_2)/(P_2)\\v_2=(0.208* 393)/(497.9)\\v_2=0.164 m^3/kg`

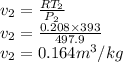
Now the work done per kg mass is given as

`w=(p_1v_1-p_2v_2)/(\gamma-1)\\w=(120* 0.491-497.9 * 0.164)/(1.3-1)\\w=-76.08 kJ/kg`

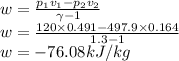
So the work done per unit kg of mass is -76.08 kJ/kg.

The heat per unit mass is given as

`Q_(poly)=(\gamma_(adi)-\gamma_(poly))/(\gamma_(adi)-1) * w_(poly)`

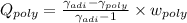
As the Argon gas is monotonic which gives γ_adiabatic=1.67

`Q_(poly)=(\gamma_(adi)-\gamma_(poly))/(\gamma_(adi)-1) * w_(poly)\\Q_(poly)=(1.67-1.3)/(1.67-1) * (-76.08 kJ/kg)\\Q_(poly)=-42.01 kJ/kg`

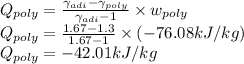
The heat transferred per unit kg of mass is -42.01 kJ/kg