Question

Steep safety ramps are built beside mountain highways to enable vehicles with defective brakes to stop safely. A truck enters a ramp at a high speed v0 and travels 690 ft in 8.5 s at constant deceleration before its speed is reduced to v0/2. Assume the same constant deceleration.a) Determine the additional time required for the truck to stop. The additional time required for the truck to stop is ______s b) the additional distance traveled by the truck is ______ft

Answer 1

a) The additional time required for the truck to stop is 8.5 seconds

b) The additional distance traveled by the truck is 230.05 ft

Step-by-step explanation:

Since the acceleration is constant, the average speed is:

(final speed - initial speed) / 2 = 0.75 v0

Since travelling at this speed for 8.5 seconds causes the vehicle to travel 690 ft, we can solve for v0:

0.75v0 * 8.5 = 690

v0 = 108.24 ft/s

The speed after 8.5 seconds is: 108.24 / 2 = 54.12 ft/s

We can now use the following equation to solve for acceleration:

`v^2 - u^2 = 2*a*s`

`54.12^2 - 108.24^2 = 2*a*690`

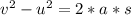
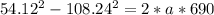
a = -6.367 m/s^2

Additional time taken to decelerate: 54.12/6.367 = 8.5 seconds

Total distance traveled:

`v^2 - u^2 = 2*a*s`

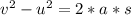
0 - 108.24^2 = 2 * (-6.367) * s

solving for s we get total distance traveled = 920.05 ft

Additional Distance Traveled: 920.05 - 690 = 230.05 ft