Question

In ΔBCD, the measure of ∠D=90°, the measure of ∠C=77°, and CD = 41 feet. Find the length of BC to the nearest foot.

Answer 1

Answer:
`x\approx182\ ft`

Explanation:

For this exercise you need to use the following Trigonometric Identity:

`cos\alpha =(adjacent)/(hypotenuse)`

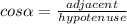
Observe the Right triangle BCD given in the exercise. You can identify that, in this case:

`\alpha =\angle C=77\°\\\\adjacent=CD=41\ ft\\\\hypotenuse=BC=x`

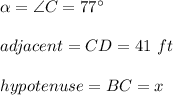
Knowing these values, you can substitute them into
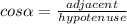`cos\alpha =(adjacent)/(hypotenuse)`, as below:

`cos(77\°)=(41)/(BC)`

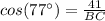
The next step is to solve for "x" in order to find its value:

`x*cos(77\°)=41\\\\x=(41)/(cos(77\°))\\\\x=182.26\ ft`

Finally, rounded the result to the nearest foot, you get that this is:

`x\approx182\ ft`