Question

Independent random samples from two regions in the same area gave the following chemical measurements (ppm). Assume the population distributions of the chemical are mound-shaped and symmetric for these two regions. Region I: ; 981 726 686 496 657 627 815 504 950 605 570 520 Region II: ; 1024 830 526 502 539 373 888 685 868 1093 1132 792 1081 722 1092 844 Let be the population mean and be the population standard deviation for . Let be the population mean and be the population standard deviation for . Determine and examine the 90% confidence interval for . Does the interval consist of numbers that are all positive? all negative? or different signs? At the 90% level of confidence, is one region more interesting that the other from a geochemical perspective?

Select one:

a. The interval contains only positive numbers. We can say at the required confidence level that one region is more interesting than the other.

b. The interval contains both positive and negative numbers. We cannot say at the required confidence level that one region is more interesting than the other.

c. The interval contains both positive and negative numbers. We can say at the required confidence level that one region is more interesting than the other. Incorrect

d. The interval contains only negative numbers. We cannot say at the required confidence level that one region is more interesting than the other.

e. The interval contains only positive numbers. We cannot say at the required confidence level that one region is more interesting than the other.

Answer 1

d. The interval contains only negative numbers. We cannot say at the required confidence level that one region is more interesting than the other.

Explanation:

Hello!

You have the data of the chemical measurements in two independent regions. The chemical concentration in both regions has a Gaussian distribution.

Be X₁: Chemical measurement in region 1 (ppm)

Sample 1

n= 12

981 726 686 496 657 627 815 504 950 605 570 520

μ₁= 678

σ₁= 164

Sample mean X[bar]₁= 678.08

X₂: Chemical measurement in region 2 (ppm)

Sample 2

n₂= 16

1024 830 526 502 539 373 888 685 868 1093 1132 792 1081 722 1092 844

μ₂= 812

σ₂= 239

Sample mean X[bar]₂= 811.94

Using the information of both samples you have to determina a 90% CI for μ₁ - μ₂.

Since both populations are normal and the population variances are known, you can use a pooled standard normal to estimate the difference between the two population means.

[(X[bar]₁-X[bar]₂)±
`Z_(1-\alpha /2)`*
`\sqrt{(Sigma^2_1)/(n1)+(Sigma^2_2)/(n_2) }`]

`Z_(1-\alpha /2)= Z_(0.95)= 1.648`

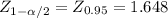
[(678.08-811.94)±1.648*
`\sqrt{(164^2)/(12)+(239^2)/(16) }`]

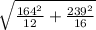[-259.49;-8.23]ppm

Both bonds of the interval are negative, this means that with a 90% confidence level the difference between the population means of the chemical measurements of region 1 and region 2 may be included in the calculated interval.

You cannot be sure without doing a hypothesis test but it may seem that the chemical measurements in region 1 are lower than the chemical measurements in region 2.

I hope it helps!