Question:
Iliana multiplied 3p – 7 and 2p^2 – 3p – 4. Her work is shown in the table.
Which is the product?
6p^3 + 23p^2 + 9p + 28
6p^3 – 23p^2 – 9p + 28
6p^3 – 23p^2 + 9p + 28
6p^3 + 23p^2 – 9p + 28
Answer:
Option C:
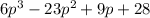 is the correct answer.
is the correct answer.
Step-by-step explanation:
The two expressions are
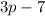 and
and
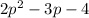
The product of the expression can be determined by multiplying each of the first term with the second term of the expression, we get,
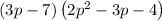
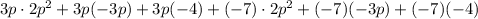
Simplifying we have,
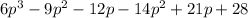
Adding the like terms, we have,
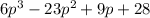
Thus, the product of the two expression is
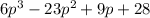
Hence, Option C is the correct answer.