Question

Which is the product?

6p3 + 23p2 + 9p + 28
6p3 – 23p2 – 9p + 28
6p3 – 23p2 + 9p + 28
6p3 + 23p2 – 9p + 28

Answer 1

c ;)

Step-by-step explanation:

Answer 2

Question:

Iliana multiplied 3p – 7 and 2p^2 – 3p – 4. Her work is shown in the table.

Which is the product?

6p^3 + 23p^2 + 9p + 28

6p^3 – 23p^2 – 9p + 28

6p^3 – 23p^2 + 9p + 28

6p^3 + 23p^2 – 9p + 28

Answer:

Option C:
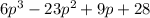`6 p^(3)-23 p^(2)+9 p+28` is the correct answer.

Step-by-step explanation:

The two expressions are
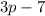`3 p-7` and
`\left2 p^(2)-3 p-4\right`

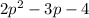
The product of the expression can be determined by multiplying each of the first term with the second term of the expression, we get,

`(3 p-7)\left(2 p^(2)-3 p-4\right)`

`3 p \cdot 2 p^(2)+3 p(-3 p)+3 p(-4)+(-7) \cdot 2 p^(2)+(-7)(-3 p)+(-7)(-4)`

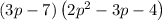
Simplifying we have,

`6p^3-9p^2-12p-14p^2+21p+28`

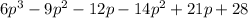
Adding the like terms, we have,

`6 p^(3)-23 p^(2)+9 p+28`

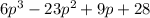
Thus, the product of the two expression is
`6 p^(3)-23 p^(2)+9 p+28`

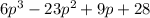
Hence, Option C is the correct answer.