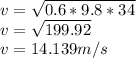Question

Suppose the coefficient of static friction between the road and the tires on a car is 0.60 and the car has no negative lift. What speed will put the car on the verge of sliding as it rounds a level curve of 34.0 m radius?

Answer 1

Speed = 14.15 m/s.

Step-by-step explanation:

Below is an attachment containing the solution.

Answer 2

14.139m/s

Step-by-step explanation:

For a body moving along a curve on a surface whose coefficient of friction is
`\mu`, the maximum velocity v the body can sustain beyond which it would skid off is given by equation (1);

`v=√(\mu gR)............(1)`

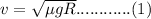
where g is acceleration due to gravity taken as
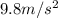`9.8m/s^2` and R is the radius of the curve.

Given;

`\mu=0.6\\R=34m`

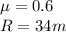
Hence'

`v=√(0.6*9.8*34) \\v=√(199.92)\\ v=14.139m/s`