Question

Six artificial satellites complete one circular orbit around a space station in the same amount of time. Each satellite has mass

m and radius of orbit L The satellites fire rockets that provide the force needed to maintain a circular orbit around the space station. The gravitational force is negligible.

Rank the net force acting on each satellite from their rockets. Rank from largest to smallest. To rank items as equivalent, overlap them.

1.m=300kg,L=7500m
2.m=200kg,L=5000m
3.m=400kg,L=2500m
4.m=800kg, L=5000m
5.m=100kg,L=10,000m
6.m=100kg,L=2500m

Answer 1

The ranking of the net force acting on different satellite from largest to smallest is
`{F_E} > {F_F} > {F_A} = {F_B} = {F_D} > {F_C}`

Step-by-step explanation:

In order to get a good understanding of this solution we need to understand that the main concepts used to solve this problem are centripetal force and velocity of satellite.

Initially, use the expression of the velocity of satellite and find out its dependence on the radius of orbit. Use the dependency in the centripetal force expression.

Finally, we find out the velocity of the six satellites and use that expression to find out the force experienced by the satellite. Find out the force in terms of mass (m) and radius of orbit (L) and at last compare the values of force experienced by six satellites.

Fundamentals

The centripetal force is necessary for the satellite to remain in an orbit. The centripetal force is the force that is directed towards the center of the curvature of the curved path. When a body moves in a circular path then the centripetal force acts on the body.

The expression of the centripetal force experienced by the satellite is given as follows:

`{F_{\rm{c}}} = \frac{{m{v^2}}}{L}`

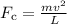
Here, m is the mass of satellite, v is the velocity, and L is the radius of orbit.

The velocity of the satellite with which the satellite is orbiting in circular path is given as follows:

`v = \frac{{2\pi L}}{T}`

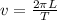
Here, T is the time taken by the satellite.

The velocity of the satellite with which the satellite is orbiting in circular path is given as follows;

`v = \frac{{2\pi L}}{T}`

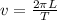
Since, all the satellites complete the circular orbit in the same amount of time. The factor of
`\frac{{2\pi }}{T}` is not affected the velocity value for the six satellites. Therefore, we can write the expression of v given as follows:

Substitute
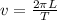`v = \frac{{2\pi L}}{T}` in the force expression
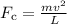`{F_{\rm{c}}} = \frac{{m{v^2}}}{L}` as follows:

`\begin{array}{c}\\{F_c} = \frac{{m{{\left( {\frac{{2\pi L}}{T}} \right)}^2}}}{L}\\\\ = \frac{{4{\pi ^2}}}{{{T^2}}}mL\\\end{array}`

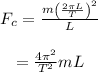
Since, all the satellites complete the circular orbit in the same amount of time. The factor of
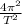`\frac{{4{\pi ^2}}}{{{T^2}}}` not affect the force value for six satellites.Therefore, we can write the expression of
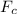`{F_c}` given as follows:

`{F_c} = kmL`

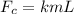
Here, k refers to constant value and equal to
`\frac{{4{\pi ^2}}}{{{T^2}}}`

`{F_A} = k{m_A}{L_A}`

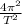
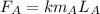
Substitute 200 kg for
`{m_A}` and 5000 m for LA in the expression
`{F_A} = k{m_A}{L_A}`

`\begin{array}{c}\\{F_A} = k\left( {200{\rm{ kg}}} \right)\left( {5000{\rm{ m}}} \right)\\\\ = {10^6}k{\rm{ N}}\\\end{array}`

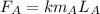
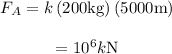
The force acting on satellite B from their rocket is given as follows:
`{F_B} = k{m_B}{L_B}`

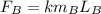
Substitute 400 kg for
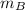`{m_B}` and 2500 m for in the expression
`{F_B} = k{m_B}{L_B}`

`\begin{array}{c}\\{F_B} = k\left( {400{\rm{ kg}}} \right)\left( {2500{\rm{ m}}} \right)\\\\ = {10^6}k{\rm{ N}}\\\end{array}`

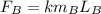
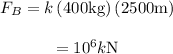
The force acting on satellite C from their rocket is given as follows:
`{F_C} = k{m_C}{L_C}`

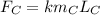
Substitute 100 kg for
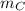`{m_C}`and 2500 m for in the above expression
`{F_C} = k{m_C}{L_C}`

`\begin{array}{c}\\{F_C} = k\left( {100{\rm{ kg}}} \right)\left( {2500{\rm{ m}}} \right)\\\\ = 0.25 * {10^6}k{\rm{ N}}\\\end{array}`

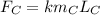
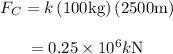
The force acting on satellite D from their rocket is given as follows:
`{F_D} = k{m_D}{L_D}`

Substitute 100 kg for
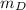`{m_D}` and 10000 m for
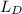`{L_D}` in the expression
`{F_D} = k{m_D}{L_D}`

`\begin{array}{c}\\{F_D} = k\left( {100{\rm{ kg}}} \right)\left( {10000{\rm{ m}}} \right)\\\\ = {10^6}k{\rm{ N}}\\\end{array}`

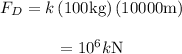
The force acting on satellite E from their rocket is given as follows:
`{F_E} = k{m_E}{L_E}`

Substitute 800 kg for
`{m_E}` and 5000 m for
`{L_E}` in the expression
`{F_E} = k{m_E}{L_E}`

`\begin{array}{c}\\{F_E} = k\left( {800{\rm{ kg}}} \right)\left( {5000{\rm{ m}}} \right)\\\\ = 4.0 * {10^6}k{\rm{ N}}\\\end{array}`

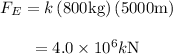
The force acting on satellite F from their rocket is given as follows:
`{F_F} = k{m_F}{L_F}`

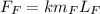
Substitute 300 kg for
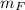`{m_F}` and 7500 m for
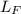`{L_F}` in the expression
`{F_F} = k{m_F}{L_F}`

`\begin{array}{c}\\{F_F} = k\left( {300{\rm{ kg}}} \right)\left( {7500{\rm{ m}}} \right)\\\\ = 2.25 * {10^6}k{\rm{ N}}\\\end{array}`

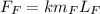
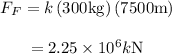
The value of forces obtained for the six-different satellite are as follows.

`\begin{array}{l}\\{F_A} = {10^6}k{\rm{ N}}\\\\{F_B} = {10^6}k{\rm{ N}}\\\\{F_C} = 0.25 * {10^6}k{\rm{ N}}\\\\{F_D} = {10^6}k{\rm{ N}}\\\\{F_E} = 4.0 * {10^6}k{\rm{ N}}\\\\{F_F} = 2.25 * {10^6}k{\rm{ N}}\\\end{array}`

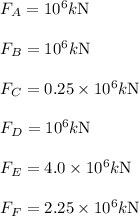
The ranking of the net force acting on different satellite from largest to smallest is
`{F_E} > {F_F} > {F_A} = {F_B} = {F_D} > {F_C}`