Question

In a taste test of a generic soda versus a brand name soda, 35% of tasters can distinguish between the colas. 30 tasters are asked to take the taste test and guess which cup contains the brand name soda. The tests are done independently in separate locations, so that the tasters do not interact with each other during the test.

a. The count of correct guesses in 30 taste tests has a Binomial distribution. What are n and p?
b. What is the mean number of correct guesses in many repetitions?
c. What is the probability of exactly 6 correct guesses?

Answer 1

a)
`n = 30, p = 0.35`

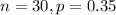
b) 10.5 correct guesses

c) 3.53% probability of exactly 6 correct guesses.

Explanation:

For each taster, there are only two possible outcomes. Either they will distinguish between the colas, or they will not. The tests are independent. So we use the binomial probability distribution to solve this problem.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

The expected value of the binomial distribution is:

`E(X) = np`

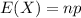
35% of tasters can distinguish between the colas.

This means that
`p = 0.35`

30 tasters are asked to take the taste test and guess which cup contains the brand name soda.

This means that
`n = 30`

a. The count of correct guesses in 30 taste tests has a Binomial distribution. What are n and p?

`n = 30, p = 0.35`

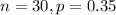
b. What is the mean number of correct guesses in many repetitions?

`E(X) = np = 30*0.35 = 10.5`

c. What is the probability of exactly 6 correct guesses?

This is P(X = 6).

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 6) = C_(30,6).(0.35)^(6).(0.65)^(24) = 0.0353`

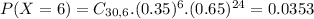
3.53% probability of exactly 6 correct guesses.