Answer:
x = 67° (nearest whole degree)
Explanation:
Sine Rule
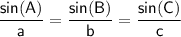
where A, B and C are the angles, and a, b and c are the sides opposite the angles
Given information
From inspection of the triangle:
- A = 38°
- a = 12
- B = x°
- b = 18
Finding x:
Substitute given values into the formula and solve for x:
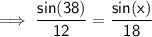
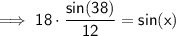
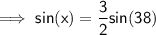
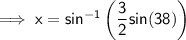
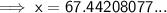
Final Solution
x = 67° (nearest whole degree)