First of all, recall that every parabola can be written as
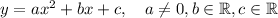
If
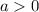 , the parabola is concave up (and thus it has a minimum value).
, the parabola is concave up (and thus it has a minimum value).
If
 , the parabola is concave down (and thus it has a maximum value).
, the parabola is concave down (and thus it has a maximum value).
So, in your case, the parabola in concave up.
The x-coordinate of the minimum can be found using
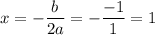
And the y-coordinate will be
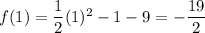
So, the minimum value is -19/2 at x=1.