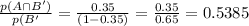Answer:
a.) The probability that A happens but B does not is 0.35
b.) The probability exactly one of these two events happens is 0.6
c.) The probability that event A happens given that event B does not happen is 0.5385.
Explanation:
The probability that event A happens , p(A) = 0.45
The probability that event B happens, p(B) = 0.35
The probability that at least one of these two events happens, P(A∪B) = 0.7
a.) The probability that A happens but B does not is
= p(A ∩ B')
= p(A) - p(A ∩ B)
= 0.45 - {p(A) + p(B) - p(A∪B)}
= 0.45 - {0.45 + 0.35 - 0.7}
= 0.45 - 0.1
= 0.35
b.) the probability exactly one of these two events happens
= p(A∩B') + p(A' ∩ B)
= P(A) + p(B) - 2p(A∪B)
= 0.45 + 0.35 - (2×0.1)
= 0.6
c.) the probability that event A happens given that event B does not happen
= p( A | B' )
=