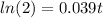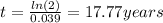Answer:
a) For 2008 we have that t = 2008-2008 = 0 and we have:
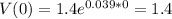
For 2022 we have that t = 2022-2008=14 and if we replace we got:
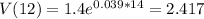
b)
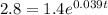
We can divide both sides by 1.4 and we got:

Now natural log on both sides:
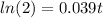
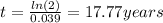
Explanation:
For this case we have the following model given:

Where V represent the exports of goods and the the number of years after 2008.
Part a
Estimate the value of the country's exports in 2008 and 2022
For 2008 we have that t = 2008-2008 = 0 and we have:
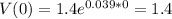
For 2022 we have that t = 2022-2008=14 and if we replace we got:
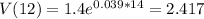
Part b
What is the doubling time for the value of the country's exports.
For this case we can set up the following condition:
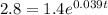
We can divide both sides by 1.4 and we got:

Now natural log on both sides: