Answer:
S = I-E.
We can find the expected value of S and we got:
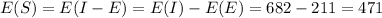
And that represent the mean of the amount of money into your savings account each month
And now we can find the variance of the random variable S like this:

And since we know that
 then we have:
then we have:
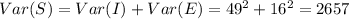
And then the deviation would be:
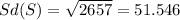
And that represent the standard deviation of the amount of money you put in your savings account each month
Explanation:
Let I the random variable that represent the income for each month and we know:
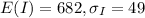
Let E the random variable that represent the monthly expenses for each month and we know:
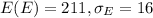
And for this case we know that the random variables I and E are independent, so then
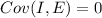
We can define the random variable S representing the amount that we can save each month and we can define S = I-E.
We can find the expected value of S and we got:
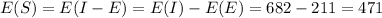
And that represent the mean of the amount of money into your savings account each month
And now we can find the variance of the random variable S like this:

And since we know that
 then we have:
then we have:
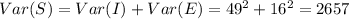
And then the deviation would be:
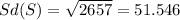
And that represent the standard deviation of the amount of money you put in your savings account each month