Answer:
- The height of the cone is 4 inches.
Solution :
We are given a cylinder and a cone of same volume i.e
 Volume of cone = Volume of cylinder
Volume of cone = Volume of cylinder
And also the diameter of the cylinder is given 4 inches
 Radius =
Radius =
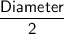
 Radius =
Radius =

 Radius = 2 inches
Radius = 2 inches
The height of cylinder is 3 inches. And the diameter of the cone is 6 inches
 Radius =
Radius =

 Radius =
Radius =

 Radius = 3 inches
Radius = 3 inches
First, let us recall the Formulas of volume of cylinder and cone:
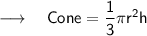

Now, we know that the volume of cone is equal to the volume of cylinder
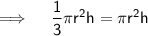
On putting the values:
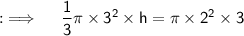
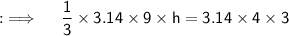
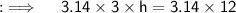
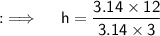
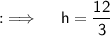

ㅤㅤㅤㅤㅤ~Hence the height of the cone is 4 inches.