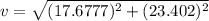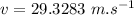Question

3. Someone at the third-floor window (12.0 m above the ground) hurls a ball downward at an angle of

45 degrees with a speed of 25 m/s. How fast will the ball be traveling when it strikes the sidewalk
below?​

Answer 1

`v=29.3283\ m.s^(-1)`

Step-by-step explanation:

Given:

• height of point from where the ball is projected,
  `h=12\ m`

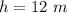
• angle of projection of the ball below the horizontal,
  `\theta=45^(\circ)`

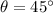
• initial velocity of projection,
  `u=25\ m.s^(-1)`

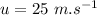
Now we find the vertical component of the initial velocity downwards:

`u_y=u.\sin\theta`

`u_y=25* \cos45^(\circ)`

`u_y=17.6777\ m.s^(-1)`

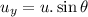
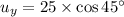
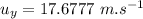
Now the final vertical velocity of the ball when it hits the ground:

using the equation of motion,

`v_y^2=u_y^2+2.g.h`

`v_y^2=17.6777^2+2* 9.8* 12`

`v_y=23.402\ m.s^(-1)`

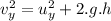
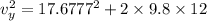
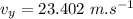
Since the horizontal component of the motion is uniform since no force acts in the horizontal direction:

`v_x=u_x=25\cos45`

`v_x=17.6777\ m.s^(-1)`

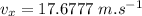
Now the resultant final velocity:

`v=√((17.6777)^2+(23.402)^2)`

`v=29.3283\ m.s^(-1)`