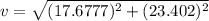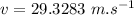Answer:
Step-by-step explanation:
Given:
- height of point from where the ball is projected,
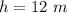
- angle of projection of the ball below the horizontal,
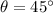
- initial velocity of projection,
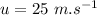
Now we find the vertical component of the initial velocity downwards:
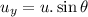
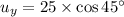
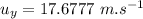
Now the final vertical velocity of the ball when it hits the ground:
using the equation of motion,
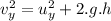
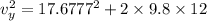
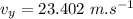
Since the horizontal component of the motion is uniform since no force acts in the horizontal direction:

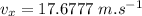
Now the resultant final velocity: