Question

A tank of final volume 10 m3 contains compressed air at 15◦C. The gage pressure in the tank is 4.50 MPa.

Evaluate the work required to fill the tank by compressing air from standard atmospheric conditions for

(a) isothermal compression and
(b) isentropic compression followed by cooling at constant pressure.

What is the peak temperature of the isentropic compression process? Calculate the energy removed during cooling for process

Answer 1

The answers to the question are as follows

(a) W = -175.6 MJ

(b) W = -329.256 MJ

The peak temperature of the isentropic compression process is 886.974 K

Step-by-step explanation:

(a) We are given the initial conditions as

v₂ = 10 m³

T₂ = 15 °C

p₂ (gauge) = 4.5 MPa gauge → 4.5 MPa + 1 atm = 4.5 MPa + 101325 Pa = 4.601 MPa

p₁ = 1 atm

Therefore isothermal compression we have the work done given by

`W_(12) = p_(2) v_(2)ln((v_(1) )/(v_(2) ) )` per unit mass of the given gas, hence

From the relation

p₁·v₁ =p₂·v₂ therefore v₁ = p₂·v₂/p₁ = 4.6 MPa× 10 m³/(1 atm) = 4.6 MPa× 10 m³/(‪101325‬ Pa) = 454.115 m³

Therefore W₁₂ = 101325 Pa × 454.11 m³× ㏑((10 m³)/(454.115 m³)) = 46013250×(-3.82) = -175575813.855 J = -175.6 MJ

W = -175.6 MJ

(b) For isentropic compression we have

W = m×cv×(T₂ -T₁)

`(p_(1) )/(p_(2) ) = ((v_(2) )/(v_(1) ) )^(K) =((T_(1) )/(T_(2) ) )^{(K)/(K-1) }`

for air we put K = 1.4

therefore we have
`(101325 )/(4601325 ) = ((10 )/(v_(1) ) )^(1.4)` from which

v₁ = 152.65 m³

We also have
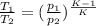`(T_(1) )/(T_(2) ) =((p_(1) )/(p_(2) ) )^{(K-1)/(K) }` or
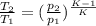`(T_(2) )/(T_(1) ) =((p_(2) )/(p_(1) ) )^{(K-1)/(K) }` from which we find the value of T₂ as
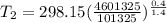`{T_(2) } =298.15( (4601325 )/(101325 ))^{(0.4)/(1.4) }` = 886.974 K (peak temperature)

Therefore from pv = RT and R =cp -cv = 1.005 -0.718 = 0.287 kJ/kg·K

Therefore number of moles = pv/(RT) = (4601325×10)(287×288.15) = 556.394 kg

m = 556.394 kg

Therefore work done at constant pressure = m·cp·(T₂-T₁) gives

556.394 kg × 1.005 kJ/kg⋅K×(298.15 K-886.974 K ) = -329256.19 kJ or -329.256 MJ

The peak temperature of the isentropic process = 886.974 K