Question

A normal distribution has a mean of 80.6 and a standard deviation of 13.9. Find the value where the lowest 5% of data ends.

Answer 1

The lowest 5% of data ends at 57.73.

Explanation:

Let the random variable X follow a Normal distribution with mean μ = 80.6 and standard deviation σ = 13.9.

The lowest 5% of the distribution can be expressed in terms of probability as follows:

`P(X<x)=0.05`

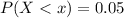
Compute the value of x as follows:

`P((X-\mu)/(\sigma)<(x-80.6)/(13.9))=0.05\\P(Z<z)=0.05`

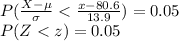
The z score such that P (Z < z) = 0.05 is z = -1.645.

**Use the z-table for the for the z-score.

The value of x is:

`z=(x-\mu)/(\sigma) \\-1.645=(x-80.6)/(13.9) \\x=80.6-(1.645*13.9)\\=57.7345\\\approx57.73`

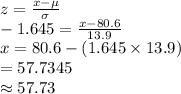
Thus, the lowest 5% of data ends at 57.73.