Answer:
The lowest 5% of data ends at 57.73.
Explanation:
Let the random variable X follow a Normal distribution with mean μ = 80.6 and standard deviation σ = 13.9.
The lowest 5% of the distribution can be expressed in terms of probability as follows:
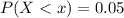
Compute the value of x as follows:
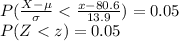
The z score such that P (Z < z) = 0.05 is z = -1.645.
**Use the z-table for the for the z-score.
The value of x is:
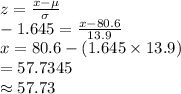
Thus, the lowest 5% of data ends at 57.73.