a) Potential in A: -2700 V
b) Potential difference: -26,800 V
c) Work:

Step-by-step explanation:
a)
The electric potential at a distance r from a single-point charge is given by:

where
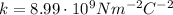 is the Coulomb's constant
is the Coulomb's constant
q is the charge
r is the distance from the charge
In this problem, we have a system of two charges, so the total potential at a certain point will be given by the algebraic sum of the two potentials.
Charge 1 is
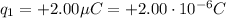
and is located at the origin (x=0, y=0)
Charge 2 is
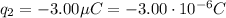
and is located at (x=0, y = 0.40 m)
Point A is located at (x = 0.40 m, y = 0)
The distance of point A from charge 1 is
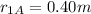
So the potential due to charge 2 is
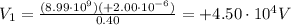
The distance of point A from charge 2 is
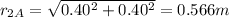
So the potential due to charge 1 is

Therefore, the net potential at point A is
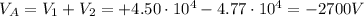
b)
Here we have to calculate the net potential at point B, located at
(x = 0.40 m, y = 0.30 m)
The distance of charge 1 from point B is
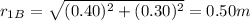
So the potential due to charge 1 at point B is

The distance of charge 2 from point B is

So the potential due to charge 2 at point B is
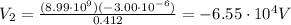
Therefore, the net potential at point B is
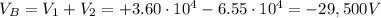
So the potential difference is
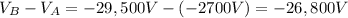
c)
The work required to move a charged particle across a potential difference is equal to its change of electric potential energy, and it is given by
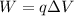
where
q is the charge of the particle
 is the potential difference
is the potential difference
In this problem, we have:
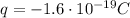 is the charge of the electron
is the charge of the electron
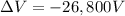 is the potential difference
is the potential difference
Therefore, the work required on the electron is
