Answer:
44,55 can be produced.
Step-by-step explanation:
First, we balanced the equation
1Cu + 2AgNO3 → 1Cu(NO3)2 + Ag
Then, we find the moles of each reagent
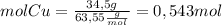
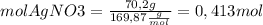
Now, we find the limiting reagent from the quantities of product that can be formed from each reagent
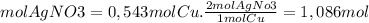
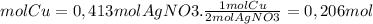
1,086 moles of AgNO3 is necessary for each mole of Cu since we have 0.413 moles of Ag(NO3), the nitrate is the limiting reagent
the value of the limiting reagent determines the amount of product that is generated
∴ 0,413 mol of Ag can be produced
Ag =
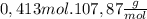 = 44,55g
= 44,55g
Ag≈ 44,6g