Question

If 34.5 g of Copper reacts with 70.2 g of silver nitrate, according to the following

reaction, what is the maximum number of grams of silver that can be

Cu + _ Ag(NO3) → Cu(NO3)2 + Ag

44. 6gAg can be produced​

Answer 1

`m_(Ag)=44.3gAg`

Step-by-step explanation:

Hello,

In this case, the first step is to write the balanced chemical reaction:

`Cu + 2 Ag(NO_3) \rightarrow Cu(NO_3)_2 + 2Ag`

Next, we find the limiting reactant, for that reason we compute the moles of copper that are available and the moles that will react with 70.2 g of silver nitrate as shown below:

`n_(Cu)^(available)=34.5gCu*(1mol Cu)/( 63.546 gCu)=0.543molCu \\n_(Cu)^(reacted \ with \ Ag(NO_3) )=70.2gAg(NO_3)*(1molAg(NO_3))/(169.87gAg(NO_3))*(1molCu)/(2molAg(NO_3)) =0.207molCu`In such a way, since there are more available moles of copper, it is in excess, so the silver nitrate is the limiting reactant, this, the maximum grams of silver result:

`m_(Ag)=0.207molCu*(2molAg)/(1molCu) *(108gAg)/(1molAg) =44.3gAg`

Best regards.

Answer 2

44,55 can be produced.

Step-by-step explanation:

First, we balanced the equation

1Cu + 2AgNO3 → 1Cu(NO3)2 + Ag

Then, we find the moles of each reagent

`mol Cu = (34,5g)/(63,55(g)/(mol) ) = 0,543 mol\\`

`mol AgNO3 = (70,2g)/(169,87(g)/(mol) ) = 0,413 mol\\`

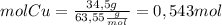
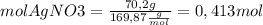
Now, we find the limiting reagent from the quantities of product that can be formed from each reagent

`mol AgNO3= 0,543mol Cu . (2 mol AgNo3)/(1 mol Cu) = 1,086 mol`

`mol Cu= 0,413 mol AgNO3 . (1 mol Cu)/(2 mol AgNO3) = 0,206 mol`

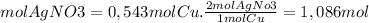
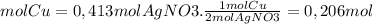
1,086 moles of AgNO3 is necessary for each mole of Cu since we have 0.413 moles of Ag(NO3), the nitrate is the limiting reagent

the value of the limiting reagent determines the amount of product that is generated

∴ 0,413 mol of Ag can be produced

Ag =
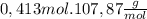`0,413 mol . 107,87(g)/(mol)` = 44,55g

Ag≈ 44,6g