Given :-
- Constant force, F = 20 N
- Mass of Car = 32 kg
- Initial speed, u = 4 m/s
- Final Speed = 9 m/s
To Find:-
- Duration for which force is appiled
Solution:-

So,

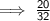
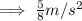
Now,
By first equation of motion -
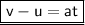
So,
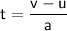
where
- v = final velocity
- u = initial velocity
- a = acceleration
- t = time duration
Putting Values -
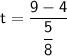
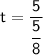
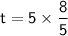
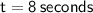
>>>Therefore, Force is applied for 8 seconds.