Answer:
Part 1) John’s situation is modeled by a linear equation (see the explanation)
Part 2)
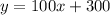
Part 3)
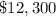
Part 4) Is a exponential growth function
Part 5)
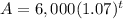
Part 6)

Part 7) Is a exponential growth function
Part 8)
 or
or
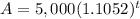
Part 9)

Part 10) Natalie has the most money after 10 years
Explanation:
Part 1) What type of equation models John’s situation?
Let
y ----> the total money saved in a jar
x ---> the time in months
The linear equation in slope intercept form

The slope is equal to
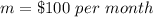
The y-intercept or initial value is
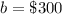
so
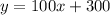
therefore
John’s situation is modeled by a linear equation
Part 2) Write the model equation for John’s situation
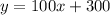
see part 1)
Part 3) How much money will John have after 10 years?
Remember that
1 year is equal to 12 months
so
10 years=10(12)=120 months
For x=120 months
substitute in the linear equation
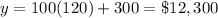
Part 4) What type of exponential model is Sally’s situation?
we know that
The compound interest formula is equal to
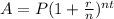
where
A is the Final Investment Value
P is the Principal amount of money to be invested
r is the rate of interest in decimal
t is Number of Time Periods
n is the number of times interest is compounded per year
in this problem we have

substitute in the formula above
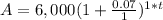
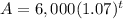
therefore
Is a exponential growth function
Part 5) Write the model equation for Sally’s situation
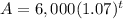
see the Part 4)
Part 6) How much money will Sally have after 10 years?
For t=10 years
substitute the value of t in the exponential growth function
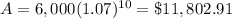
Part 7) What type of exponential model is Natalie’s situation?
we know that
The formula to calculate continuously compounded interest is equal to
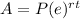
where
A is the Final Investment Value
P is the Principal amount of money to be invested
r is the rate of interest in decimal
t is Number of Time Periods
e is the mathematical constant number
we have
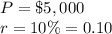
substitute in the formula above

Applying property of exponents
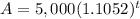
therefore
Is a exponential growth function
Part 8) Write the model equation for Natalie’s situation
 or
or
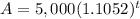
see Part 7)
Part 9) How much money will Natalie have after 10 years?
For t=10 years
substitute
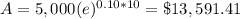
Part 10) Who will have the most money after 10 years?
Compare the final investment after 10 years of John, Sally, and Natalie
Natalie has the most money after 10 years