Answer:
a)36 lb
b) 40 in
Step-by-step explanation:
Given that;
Weight of the cabinet (W) = 120 lb
co-efficient of friction (μ) = 0.30
The force P required to move the cabinet to the right can be determined by the following:
Equilibrium Equation
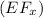 along the horizontal direction to the right is equal to zero.
along the horizontal direction to the right is equal to zero.
Fricitonal force (F) = μN
where μ = co-efficient of friction & N = normal reaction
Now;
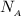 +
+
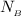 - W = 0
- W = 0
W =
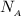 +
+
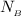
W = weight of the cabinet
So for locked caster A and B , the normal reaction are
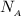 and
and
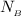 respectively.
respectively.
Since;
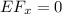

where:
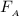 = frictional force for caster A; &
= frictional force for caster A; &
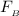 = frictional force for caster B
= frictional force for caster B
So, that implies that;
P - μ
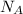 - μ
- μ
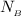 = 0
= 0
P = μ
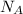 + μ
+ μ
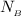
P = μ
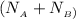
we can as well say taht:
P = μW since W =
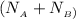
P = 0.3 × 120 lb
P = 36 lb
We can now say that, the force P required to move the cabinet to the right = 36 lb
b)
Determine; The largest allowable value of h if the cabinet is not to tip over.
So if the cabinet tip over point B where it is being locked, point A definitely loses contact with the ground.
Then there exist no reaction exerted by the ground surface at point A.
So, we have to take a look at the moment equilibrium equation about point B which can be represented as:
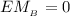
=
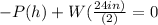 (since the difference between
(since the difference between
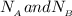 = 24 in
= 24 in
h =
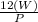
If W = 120lb and P = 36 lb
then h =

h = 40 in
∴ The largest allowable value of h if the cabinet is not to tip over = 40 in