Question

Water flows downward through a vertical 10-mm-diameter galvanized iron pipe with an average velocity for 5.0 m/s and exits as a free jet. There is a small hole in the pipe 4 meters above the outlet. Will water leak out of the pipe through this hole, or will air enter into the pipe through the hole? Repeat the problem if the average velocity is 0.5 m/s.

Answer 1

In case of 5 m/s:

`P_1=0.045*(4)/(0.01)*9800*((5)^2)/(2*9.8)-9800*4\\ P_1=185800 N/m^2=1.85800*10^5 N/m^2`

`P_1`>
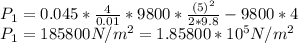
`P_2` i.e
`P_1`>0, It means Water will leak out of hole.

In case of 0.5 m/s:

`P_1=0.052*(4)/(0.01)*9800*((0.5)^2)/(2*9.8)-9800*4\\ P_1=-36600N/m^2=-3.6600*10^4 N/m^2`

`P_1`<
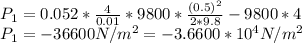
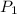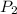`P_2` i.e
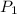`P_1`<0. It means air will enter into the pipe.

Step-by-step explanation:

Note:

Values of constant v,f and
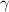`\gamma` can vary according to the conditions. Value taken below are taken from water properties table.

According to Bernoulli Equation: Considering the frictional affects
`(fL)/(D)`

`(P_1)/(\gamma)+(V^2_1)/(2g)+z_1= (P_2)/(\gamma)+(V^2_2)/(2g)+(fL)/(D)(V^2_2)/(2g)+z_2`

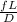
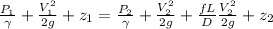
Where:

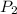`P_2` is the pressure at other end of pipe(outlet)=0

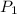`P_1` is the pressure at hole

`V_1=V_2=V`

`z_1=4 m\\z_2=0`

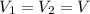
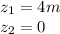
Above equation will become:
`(P_1)/(\gamma)= (fL)/(D)(V^2_2)/(2g)-z_1`

`L=z_1`

`{P_1} = \gamma(fL)/(D)(V^2_2)/(2g)-{\gamma}z_1`

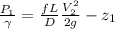
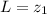
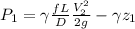
Calculating Re number:

`Re=(VD)/(v)`

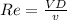
Where:

V is the velocity

D is the diameter

v is the kinematic viscosity of water. Lets consider it
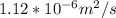`1.12*10^(-6)m^2/s`. However kinematic viscosity can be taken according to temperature.

In case of 5 m/s:

Re=
`(5*0.01)/(1.12*10^(-6))=44642.85`

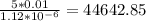
For galvanized iron pipe , Roughness coefficient ε is 0.15 mm

`(\epsilon)/(D)=(0.15)/(10)=0.015`

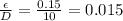
From Moody Charts, At above Re and
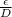`(\epsilon)/(D)`, Value of friction coefficient f is≈0.045.

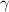`\gamma`≈9800 N/m^2

`P_1=0.045*(4)/(0.01)*9800*((5)^2)/(2*9.8)-9800*4\\ P_1=185800 N/m^2=1.85800*10^5 N/m^2`

`P_1`>
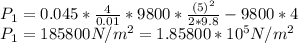
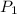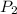`P_2` i.e
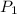`P_1`>0, It means Water will leak out of hole.

In case of 0.5 m/s:

Same above Procedure:

Calculating Re:

Re=
`(0.5*0.01)/(1.12*10^(-6))=4464.285`

`(\epsilon)/(D)=(0.15)/(10)=0.015`

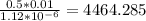
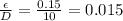
From Moody Charts, At above Re and
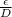`(\epsilon)/(D)`, Value of friction coefficient f is≈0.052.

`P_1=0.052*(4)/(0.01)*9800*((0.5)^2)/(2*9.8)-9800*4\\ P_1=-36600N/m^2=-3.6600*10^4 N/m^2`

`P_1`<
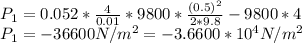
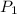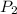`P_2` i.e
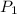`P_1`<0. It means air will enter into the pipe.