Question

A stream of hot wat at 85 deg C at a rate of 1 kg/s is needed for the pasteurizing unit in a milk bottling plant. Such a stream is not readily available, and will be produced in a well-insulated mixing tank by directly injecting st rem from a boiler plant at 10 bar and 200 deg C into city water available at 1 bar and 20 deg C. a) Calculate the flow rates of city water and stream needed. b) Calculate the rate of entropy production in the mixing tank. Any help would be greatly appreciated

Answer 1

the flow rate for steam from the boiler plant =
`0.099kg/s`

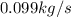
the flow rate from the city water = 0.901 kg/s

the rate of entropy production in the mixing tank = 0.2044 kJ/k

Step-by-step explanation:

In a well-insulated mixing tank where:

`Q_(cv) = 0` &
`W_(cv)=0`

The mass flow rates can be calculated using the formula:

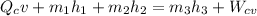`Q_cv+m_1h_1+m_2h_2=m_3h_3+W_{cv` ------ equation (1)

so;

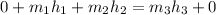`0+m_1h_1+m_2h_2=m_3h_3+0` ------- equation (2)

Given that:

From the steam in the boiler plant;

The temperature (T₁) = 200°C

Pressure (P₁) = 10 bar

The following data from compressed water and super-heated steam tables were also obtained at: T₁ = 200°C

h₁ = 2828.27 kJ/kg

s₁ = 6.95 kJ/kg K

m₁ (flow rate for steam in the boiler plant) = ????

Also, for city water

The temperature (T₂) = 20°C

Pressure (P₂) = 1 bar

Data obtained from compressed water and super-heated steam tables are as follows:

h₂ = 84.01 kJ/kg

s₂ = 0.2965 kJ/kg K

m₂ (flow rate for city water) = ???

For stream of hot wat at 85 deg C

Temperature (T₃) = 85°C

h₃(
`h_f`) = 355.95 kJ/kg

s₃(
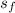`s_f`) = 1.1344 kJ/kg K

m₃ = 1 kg/s

so since:

m₁ + m₂ = m₃ (since m₃ = 1)

m₂ = 1 - m₁

From equation (2);

`0+m_1h_1+m_2h_2=m_3h_3+0`

=
`m_1(2828.27)+(1-m_1)(84.01)=1(355.95)`

=
`2828.27m_1+(84.01-84.01m_1)=(355.95)`

=
`2828.27m_1-84.01m_1=355.95-84.01`

=
`m_1(2828.27-84.01)=355.95-84.01`

`m_1 = (355.95-84.01)/(2828.27-84.01)`

`m_1 = (271.94)/(2744.26)`
`m_1 = 0.099 kg/s`

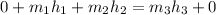
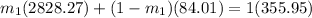
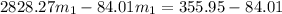
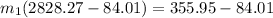
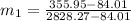
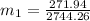
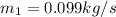
∴ the flow rate for steam from the boiler plant =
`0.099kg/s`

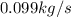
since; m₂ = 1 - m₁

m₂ = 1 - 0.099 kg/s

m₂ = 0.901 kg/s

∴ the flow rate from the city water = 0.901 kg/s

b)

rate of entropy production in the mixing tank can be determined using the formula:

Δ
`S_(production) = m_3}s_3-(m_1s_1+m_2s_2)`

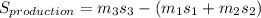
Δ
`S_(production)`
`= (1)(1.1344)-(0.099)(6.6955)-0.901(0.2965)`

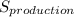
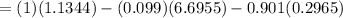
Δ
`S_(production)`
`= 1.1344-0.6628545-0.2671465`

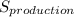
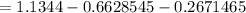
Δ
`S_(production)`
`= 1.1344 - 0.930001`

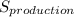
Δ
`S_(production)`
`= 0.204399`

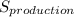
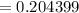
Δ
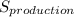`S_(production)` ≅ 0.2044 kJ/k

∴ the rate of entropy production in the mixing tank = 0.2044 kJ/k