Answer:
The magnitude is 47.0 and the direction is 120.7° above the x-axis counterclockwise.
Step-by-step explanation:
Hi there!
The magnitude of any vector is calculated as follows:
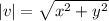
Where:
v = vector.
x = x-component of v.
y = y-component of v.
Then, the magnitude of this vector will be:
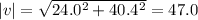
The magnitude is 47.0
The direction can be found by trigonometry (see attached figure).
According to the trigonometry rules of right triangles (as the one in the figure):
cos θ = adjacent side to the angle θ / hypotenuse
In this case:
adjacent side = x-component of v.
hypotenuse = magnitude of v.
Then:
cos θ = 24.0 / 47.0
θ = 59.3°
Measured in counterclockwise:
180° - 59.3° = 120.7°
The magnitude is 47.0 and the direction is 120.7° above the x-axis counterclockwise.