Answer:
The probability that there was no messages received during a 2-hour period is 0.3679.
Explanation:
Let the random variable X = time between the arrival of e-mail messages.
The random variable
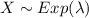
The probability distribution function of exponential distribution is:
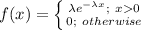
The mean of the distribution is, Mean = 2.
The value of λ is:

Compute the probability that there was no messages received during a 2-hour period as follows:
![P(X>2)=1-P(X\leq 2)\\=1-\int\limits^(2)_(0) {\lambda e^(-\lambda x)} \, dx \\=1-\lambda[(e^(-\lambda x))/(-\lambda) ]^(2)_(0)\\=1-[1-e^{-(x)/(2) }]^(2)_(0)\\=1-[1-e^{-(2)/(2)}]\\=e^(-1)\\=0.3679](https://img.qammunity.org/2021/formulas/mathematics/college/st0g8fv4w9urrfpns4v7cj7xuuhqp644ti.png)
Thus, the probability that there was no messages received during a 2-hour period is 0.3679.