Question

A high-profile consulting company chooses its new entry-level employees from a pool of recent college graduates using a five-step interview process. Unfortunately, there are usually more candidates who complete the interview process than the number of new positions that are available. As a result, cumulative GPA is used as a tie-breaker. GPAs for the successful interviewees are Normally distributed with a mean of 3.3 and a standard deviation of 0.4. Out of 163 people who made it through the interview process, only 121 can be hired. What cut-off GPA should the company use?

a. 3.00
b. 3.04
c. 3.08
d. 3.12

Answer 1

Option B) 3.04

Explanation:

We are given the following in the question:

Number of people interviewed,n = 163

Number of people hire, x = 121

Proportion of people hire =

`(x)/(n) = (121)/(163) = 0.742`

Mean, μ = 3.3

Standard Deviation, σ = 0.4

We are given that the distribution of GPA for the successful interviewees is a bell shaped distribution that is a normal distribution.

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

We have to find the value of x such that the probability is 0.742

`P( X > x) = P( z > \displaystyle(x - 3.3)/(0.4))=0.742`

`= 1 -P( z \leq \displaystyle(x - 3.3)/(0.4))=0.742`

`=P( z \leq \displaystyle(x - 3.3)/(0.4))=0.258`

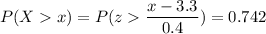
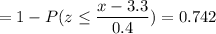
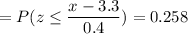
Calculation the value from standard normal z table, we have,

`\displaystyle(x - 3.3)/(0.4) = -0.650\\\\x = 3.04`

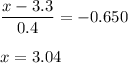
Thus, cut-off GPA should be 3.04.

Option B) 3.04