Question

Consider a test for using a particular drug. The test will produce 99% true positive results for drug users and 99% true negative results for non-drug users. Suppose that 0.5% of people are users of the drug. What is the probability that a randomly selected individual with a positive test is a drug user?

Answer 1

Explanation:

Using Bayes' theorem, we have:

`P(A|B)= (P(B|A)P(A))/(P(B))`

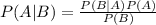
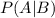`P(A|B)` is a conditional probability: the likelihood of event A occurring, given that B is true.

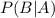`P(B|A)` is also a conditional probability: the likelihood of event B occurring, given that A is true.

P(A) and P(B) are the marginal probabilities of observing A and B, independently of each other.

We solve thus:

`P(User|+) = (P(+|User)P(User))/(P(+))`

=
`(P(+|User)P(User))/(P(+|User)P(User) + P(+|Non-user)P(Non-user))`

=
`(0.99 X 0.005)/(0.99 X 0.005 + 0.01 X 0.995)`

=
`(0.00495)/(0.00495 + 0.00995)`

=
`(0.00495)/(0.0149)`

=
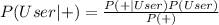
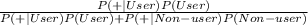
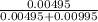
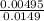
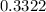`0.3322` or
`33.22%`%

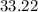Therefore, if an individual tests positive, it is more likely than not (1 - 33.2% = 66.8%) that they do not use the drug.