Question

Option A: Base salary of 11,000 a year with a commission of 16 percent of your sales. Option B base salary of 20,000 a year with a commission of 5 percent of your sales. How much jewelry would you need to sell for option A to produce a larger income. Round tor answer to the nearest cent.

Answer 1

More than $81,818.18

Explanation:

Let x represent amount of sales.

We have been given that option A offers a base salary of 11,000 a year with a commission of 16 percent of your sales.

Total income using option A would be
`A(x)=0.16x+11,000`

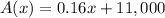
We are also told that option B offers a base salary of 20,000 a year with a commission of 5 percent of your sales.

Total income using option B would be:
`B(x)=0.05x+20,000`

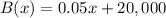
To solve our given problem, we need to solve for x such that
`A(x)>B(x)`.

`0.16x+11,000>0.05x+20,000`

`0.16x-0.05x>20,000-11,000`

`0.11x>9,000`

`(0.11x)/(0.11)>(9,000)/(0.11)`

`x>81,818.1818`

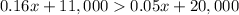
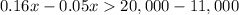
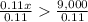
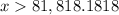
Therefore, in order to produce larger income for option A, you will have to sell more than $81,818.18.