Question

The soccer league in 1 community has 8 teams. You are required to​ predict, in​ order, the top 3 teams at the end of the season. Ignoring the possibility of​ ties, calculate the number of different predictions you could make. What is the probability of making the correct prediction by​ chance?

Answer 1

336 different predictions.

1/336 probability of making the correct prediction by​ chance

Explanation:

The order is important.

For example, Team A, B and C is a different outcome than team B, A, C.

So we use the permutations formula to solve this problem:

Permutations formula:

The number of possible permutations of x elements from a set of n elements is given by the following formula:

`P_((n,x)) = (n!)/((n-x)!))`

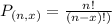
In this problem, we have that:

Permutations of 3 from a set of 8. So

`P_((8,3)) = (8!)/((8-3)!) = 336`

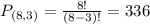
What is the probability of making the correct prediction by​ chance?

There are 336 possible outcomes.

By chance, you predict 1.

So there is a 1/336 probability of making the correct prediction by​ chance