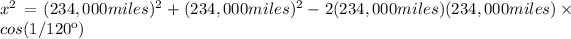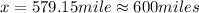Question

suppose a laser beam directed toward the visible center of the moon misses its assign target by 30 seconds . How far in miles from its assigned target is it. ( use 234000) miles as the distance from the surface of the earth to the surface of the moon)

Answer 1

• Approximately 600 miles

Step-by-step explanation:

There are several ways to solve this using different assumptions.

First you need to imagine an isosceles triangle formed by:

• the equal sides of the triangle are the distance between the Earth and the Moon: 234,000 miles

• the included angle is 30 second of degree

• the base side of the triangle, opposed to the 30 seconds angle, is how far in miles from its assigned target the laser beam is: x

You can solve for x in several ways.

I will use the cosine rule:

`c^2=a^2+b^2-2accos(\alpha)`

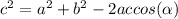
Where:

`c=x\\\\a=234,000miles\\\\b=234,000miles\\\\\alpha=30seconds`

One second of degree equals 1/3600 degrees:

`30seconds* 1degree/3600seconds=1/120degrees`

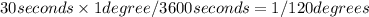
Substitute in the equation and compute:

`x^2=(234,000miles)^2+(234,000miles)^2-2(234,000miles)(234,000miles)* cos(1/120\º)`

`x=579.15mile\approx600miles`