Answer:
Part a: The temperature of the mixture at 160kPA is 257.68K.
Part b:The specific enthalpy of the mixture as it exits the system is 237.97 kJ/kg.
Part c:The entropy change for the mixture is 0.6999kJ/K
Part d: The total entropy change is 0.027 kJ/K
Step-by-step explanation:
Part a
The temperature is as viewed from the the table of Saturated properties for the Refrigerant 134a for Pressure of 160kPa.

The temperature of the mixture at 160kPA is 257.68K
Part b
For specific enthalpy from the same table of Saturated properties for the Refrigerant 134a for Pressure of 160kPa for the vapour phase which is given as
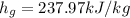
The specific enthalpy of the mixture as it exits the system is 237.97 kJ/kg.
Part c
The entropy change for the mixture is given as
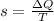
Here
ΔQ is the heat in which is given as 180kJ
T is the temperature of the mixture which is calculated in part a as 257.28K
so the equation becomes.

The entropy change for the mixture is 0.6999kJ/K
Part d
For overall entropy change, the entropy change in the cooled space is also to be calculated such that
Q is the heat in which is given as 180kJ
T is the temperature of the cooled space which is given as -5°C or 268K
so the equation becomes.
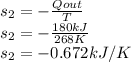
So the total entropy change is
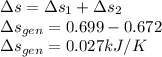
The total entropy change is 0.027 kJ/K