Question

A 500-page book contains 250 sheets of paper. The thickness of the paper used to manufacture the book has mean 0.08 mm and standard deviation0.01mm. What is the probability that a randomly chosen book is more than 20.2 mm thick (not including the covers)

Answer 1

Probability = 0.1038 or 10.38%

Explanation:

Given,

Number of sheets n = 250

Mean
`\mu =0.08`

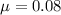
Standard deviation
`\sigma =0.01`

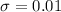
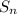`S_(n)` = Sum of sample items.

From the Central Limit Theorem we get,
`S_(n)`~
`N(n\mu ,n\sigma^2)`

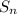n\mu = 250 × 0.08

= 20

`\sigma^2S_(n)=n\sigma^2`

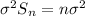
= 250(0.01)²

= 0.025

Therefore,
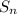`S_(n)`~N(20,0.025)

The Z-value corresponding to 20.2 :

`Z=(20.2-20)/(√(0.025))`

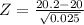
= 1.26

Finally,
`P(S_(n)>20.2)=P(z>1.26)`

= 1 - 0.8962

= 0.1038

Probability = 0.1038 or 10.38%