Question

A car dealership sells an average of 10 cars in a day. Using the Poisson​ model, what is the probability that the dealer sells 8 cars​ tomorrow?

Answer 1

P(X=8)=11.2599 %

Explanation:

According to the Poisson Model:

P=
`(e^(-\lambda)\lambda^(x))/(x!)`

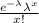
where:

λ is the average of cars sold

x is the number of cars sold tomorrow

P is the probability of cars sold tomorrow

In our case:

Given data:

λ=10 cars

x=8 cars

Required:

The probability that the dealer sells 8 cars​ tomorrow=?

Solution:

`P=(e^(-\lambda)\lambda^(x))/(x!)\\ P=(e^(-10)10^(8))/(8!)\\P=0.112599\\P=11.2599\%`

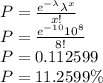
P(X=8)=11.2599 %