Question

From a survey of coworkers you find that 36​% of 200 have already received this​ year's flu vaccine. An approximate 95​% confidence interval is ​(0.293​, 0.427​). ​a) How would the confidence interval change if the sample size had been 1800 instead of 200​? ​b) How would the confidence interval change if the confidence level had been 90​% instead of 95​%? ​c) How would the confidence interval change if the confidence level had been 98​% instead of 95​%?

Answer 1

Part a: By increasing the sample size for same confidence level, the confidence interval is reduced.

Part b: By reducing the confidence level for same sample size, the confidence interval is reduced.

Part c: By increasing the confidence level for same sample size, the confidence interval is increased.

Step-by-step explanation:

Part a

As from given data

• Percentage of co-workers already received flu vaccine p=0.36,
• n=1800

The confidence interval is given as

`CI=\hat{p} \pm z_(\alpha)\sqrt{(p(1-p))/(n)}`

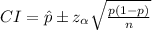
Here

• z is given for 95% confidence level as 1.960

By substituting values in the equation

`CI=\hat{p} \pm z_(\alpha)\sqrt{(p(1-p))/(n)}\\CI=0.36 \pm 1.960\sqrt{(0.36(1-0.36))/(1800)}\\CI=0.36 \pm 0.02217\\CI=(0.3378,0.3812)`

It is evident that the confidence interval is smaller, indicating a lesser chance of error.

This means that by increasing the sample size for same confidence level, the confidence interval is reduced.

Part b

As from given data

• Percentage of co-workers already received flu vaccine p=0.36,
• n=200

The confidence interval is given as

`CI=\hat{p} \pm z_(\alpha)\sqrt{(p(1-p))/(n)}`

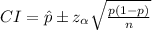
Here

• z is given for 90% confidence level as 1.645

By substituting values in the equation

`CI=\hat{p} \pm z_(\alpha)\sqrt{(p(1-p))/(n)}\\CI=0.36 \pm 1.645\sqrt{(0.36(1-0.36))/(200)}\\CI=0.36 \pm 0.0557\\CI=(0.3043,0.4157)`

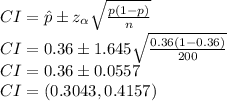
It is evident that the confidence interval is smaller, as the confidence level is reduced.

This means that by reducing the confidence level for same sample size, the confidence interval is reduced.

Part c

As from given data

• Percentage of co-workers already received flu vaccine p=0.36,
• n=200

The confidence interval is given as

`CI=\hat{p} \pm z_(\alpha)\sqrt{(p(1-p))/(n)}`

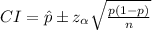
Here

• z is given for 98% confidence level as 2.33

By substituting values in the equation

`CI=\hat{p} \pm z_(\alpha)\sqrt{(p(1-p))/(n)}\\CI=0.36 \pm 2.33\sqrt{(0.36(1-0.36))/(200)}\\CI=0.36 \pm 0.07899\\CI=(0.2810,0.4389)`

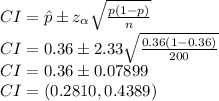
It is evident that the confidence interval is greater, as the confidence level is increased.

This means that by increasing the confidence level for same sample size, the confidence interval is increased.