Question

Assume your computer is able to complete 4 double floating-point operations per cycle when operands are in registers and it takes an additional delay of 100 cycles to access any operands that are not in registers. The clock frequency of your computer is 2 Ghz.

Answer 1

For 1st algorithm: The total run time is 200.25 s, while that of total waste time is 200 sec and the percentage of the waste time is 99.8%.

For 2nd algorithm:The total run time is 100.35 s, while that of total waste time is 100.1 sec and the percentage of the waste time is 99.75%.

Step-by-step explanation:

As the complete question is not visible, therefore, the question is searched online and following reference question is obtained.

Following data is given as

Floating point operation time=T/4

Memory Access Time =100T

Frequency =2 GHz

Number of Cycles=1000

1st Algorithm

/*dgemm0: simple ijk version triple loop

algorithm*/

for (i=0; i<n; i++)

for (j=0; j<n; j++)

for (k=0; k<n; k++)

c[i*n+j] += a[i*n+k] * b[k*n+j];

First by rewriting the operation inside the inner loop:

= + ×

Now first A, B and C are loaded into the registers so

`Load \,Time=3 * Memory \,Access \,Time=3 * 100\, T =300\, T`

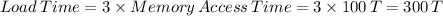
For 2 floating point computations (addition and multiplication)

`Computation\, Time=2 * Floating\, Time\\Computation\, Time=2 * (T)/(4)\\Computation\, Time=(T)/(2)`

Finally, to store and repeat the cycle as N^3 times the time is estimated as

`Store \,Time=Memory\, Access\, Time=100T`

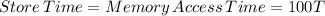
Total Run time is given as

`T_(run)=N^3 * [T_(load)+T_(comp)+T_(store)]\\T_(run)=1000^3 * [300T+(T)/(2)+100T]\\T_(run)=1000^3 * [400.5T]\\T_(run)=200.25 s`

Total Wasted time is given as

`T_(waste)=N^3 * [T_(load)+T_(store)]\\T_(waste)=1000^3 * [300T+100T]\\T_(waste)=1000^3 * [400T]\\T_(waste)=200 s`

Percentage of Waste time is given as

`\%age \, waste=(T_(waste))/(T_(run))* 100\\\%age \, waste=(200)/(200.25)* 100\\\%age \, waste=99.8\%`

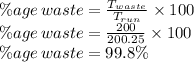
The total run time is 200.25 s, while that of total waste time is 200 sec and the percentage of the waste time is 99.8%.

2nd Algorithm

/*dgemm1: simple ijk version triple loop

algorithm with register reuse*/

for (i=0; i<n; i++)

for (j=0; j<n; j++) {

register double r = c[i*n+j];

for (k=0; k<n; k++)

r += a[i*n+k] * b[k*n+j];

c[i*n+j] = r;

}

Initialize register r with the content of C for N2 Times as given as
`Initialization\,Time=N^2 * Memory \,Access \,Time=N^3 * 100\, T`

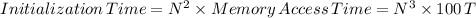
Time for Loading Operands A and B into registers for N3 Times is given as

`Load \,Time=N^3 * 2 * Memory \,Access \,Time=N^3* 2 * 100\, T =N^3* 200\, T`

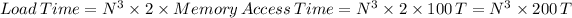
For 2 floating point computations (addition and multiplication)

`Computation\, Time=N^3 *(T)/(2)`

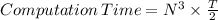
Final Memory update to store result in the register r to the memory for N2 Times

`Store \,Time=Memory\, Access\, Time=N^2 * 100T`

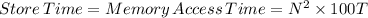
Total Run time is given as

`T_(run)=N^3 * [T_(load)+T_(comp)]+N^2 * [T_(linit)+T_(store)]\\T_(run)=1000^3 * [200T+(T)/(2)]+1000^2 * [100T+100T]\\T_(run)=1000^3 * [200.5T]+1000^2 * [200T]\\T_(run)=100.35 s`

Total Wasted time is given as

`T_(waste)=N^3 * [T_(load)]+N^2 * [T_(init)+T_(store)]\\T_(waste)=1000^3 * [200]+1000^2 * [100T+100T]\\T_(waste)=1000^3 * [200T]+1000^2 * [200T]\\T_(waste)=100.1 s`

Percentage of Waste time is given as

`\%age \, waste=(T_(waste))/(T_(run))* 100\\\%age \, waste=(100.1)/(100.35)* 100\\\%age \, waste=99.75\%`

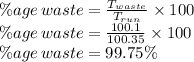
The total run time is 100.35 s, while that of total waste time is 100.1 sec and the percentage of the waste time is 99.75%.