Question

can anyone help me with this please.i have the current and pf for branch 1 and 2 but cant figure out the total current, pf and angle. thanks

Answer 1

• branch 1: i = 25.440∠-32.005°; pf = 0.848 lagging
• branch 2: i = 21.466∠63.435°; pf = 0.447 leading
• total: i = 31.693∠10.392° leading; pf = 0.984 leading

Step-by-step explanation:

To calculate the currents in the parallel branches, we need to know the impedance of each branch. That will be the sum of the resistance and reactance.

The inductive reactance is ...

`X_L=j\omega L=j2\pi fL=j100\pi\cdot 15.915*10^(-3)\approx j4.99984\,\Omega`

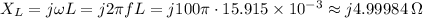
The capacitive reactance is ...

`X_C=(1)/(j\omega C)=(-j)/(100\pi\cdot 318.31*10^(-6)F)\approx -j10.00000\,\Omega`

Branch 1

The impedance of branch 1 is ...

Z1 = 8 +j4.99984 Ω

so the current is ...

I1 = V/Z = 240/(8 +j4.99984) ≈ 25.440∠-32.005°

The power factor is cos(-32.005°) ≈ 0.848 (lagging)

Branch 2

The impedance of branch 2 is ...

Z2 = 5 -j10 Ω

so the current is ...

I2 = 240/(5 +j10) ≈ 21.466∠63.435°

The power factor is cos(63.436°) ≈ 0.447 (leading)

Total current

The total current is the sum of the branch currents. A suitable calculator can add these vectors without first converting them to rectangular form.

It = I1 +I2 = (21.573 -j13.483) +(9.6 +j19.2)

It ≈ 31.173 +j5.717 ≈ 31.693∠10.392°

The power factor for the circuit is cos(10.392°) ≈ 0.984 (leading)

__

The phasor diagram of the currents is attached.

_____

Additional comment

Given two vectors, their sum can be computed several ways. One way to compute the sum is to use the Law of Cosines. In this application, the angle between the vectors is the supplement of the difference of the vector angles: 84.560°.