Question

Given a 5x5 matrix for Playfair cipher a. How many possible keys does the Playfair cipher have? Ignore the fact that some keys might produce identical encryption results. Express your answer as an approximate power of 2. b. Now take into account the fact that some Playfair keys produce the same encryption results. How many effectively unique keys does the Playfair cipher have?

Answer 1

a. 25! =
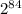`2^(84)`(Approximately)

b. 24!

Step-by-step explanation:

a. For a Playfair cipher, we have 25 possible keys as it is arranged in a 5 * 4 matrix. Based on permutation to find all the possible arrangement, we have: 25! = 1.551121004×10²⁵ =
`2^(84)`

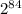
We actually have 26 letters as key to re-arrange in a playfair cipher of letter 'i' and letter 'j' are counted as one.

b. Given any 5x5 configuration, any of the four row rotations is equivalent, for a total of five equivalent configurations. For each of these five configurations, any of the four column rotations is equivalent. So each configuration in fact represents 25 equivalent configurations. Thus, the total number of unique keys is:

25!/25 = 24! = 6.204484017×10²³