Question

Four of the minterms of the completely specified function f(a, b, c, d) are m0, m1, m4, and m5.

(a) Specify additional minterms for f so that f has eight prime implicants with two literals and no other prime implicants.
(b) For each prime implicant, give its algebraic

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

a) The required additional minterms for f so that f has eight primary implicants with two literals and no other prime implicant are
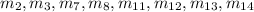`m_(2),m_(3),m_(7),m_(8),m_(11),m_(12),m_(13),m_(14)` and
`m_(15)`

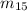
b) The essential prime implicant are
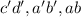`c' d',a'b',ab` and
`cd`

c) The minimum sum-of-product expression for f are

`a'b' +ab +c'd'+cd+a'c',\\ a'b'+ab+c'd'+cd+a'd,\\a'b'+ab+c'd'+cd+bc' and \\ a'b'+ab+c'd' +cd+bd`

Step-by-step explanation:

The explanation is shown on the second third and fourth image